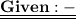








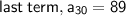






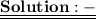
The nth term of A.P is determined by the formula-

where
Since ,


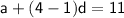

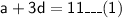
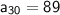



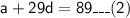
Subtracting equation (1) from equation(2)
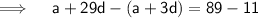
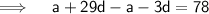
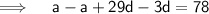
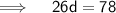


Putting the value of d in equation (1) -
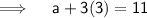
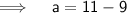

- Second term of A.P.,
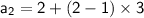
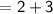
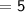
- Third term of A.P.,
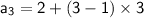
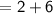

 Thus , The A.P is 2,5,8,. . . . . .
Thus , The A.P is 2,5,8,. . . . . .
Now,

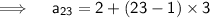
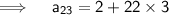
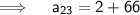
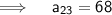
 Thus , 23rd term is 68.
Thus , 23rd term is 68.