Question

asked Apr 25, 2022 157k views

1 Answer

Ksice · Answer 1 · 2022-04-30T08:56:21+0000

Answer:

a) 0.513 = 51.3% probability that a randomly selected voter in the town supports the tax increase.

b) 0.487 = 48.7% probability that a randomly selected voter does not support the tax increase.

c) 0.1777 = 17.77% probability he or she is a registered Independent.

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

$P(B|A) = (P(A \cap B))/(P(A))$

In which

P(B|A) is the probability of event B happening, given that A happened.

$P(A \cap B)$ is the probability of both A and B happening.

P(A) is the probability of A happening.

Question a:

57% of 46%(democrats)

38% of 42%(republicans)

76% of 12%(independents)

So

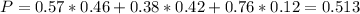
P = 0.57*0.46 + 0.38*0.42 + 0.76*0.12 = 0.513

0.513 = 51.3% probability that a randomly selected voter in the town supports the tax increase.

Question b:

1 - 0.513 = 0.487

0.487 = 48.7% probability that a randomly selected voter does not support the tax increase.

c. Suppose you find a voter at random who supports the tax increase. What is the probability he or she is a registered Independent?

Event A: Supports the tax increase.

Event B: Is a independent.

0.513 = 51.3% probability that a randomly selected voter in the town supports the tax increase.

This means that
P(A) = 0.513

Probability it supports a tax increase and is a independent:

76% of 12%, so:

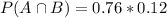
$P(A \cap B) = 0.76*0.12$

Thus

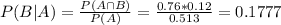
$P(B|A) = (P(A \cap B))/(P(A)) = (0.76*0.12)/(0.513) = 0.1777$

0.1777 = 17.77% probability he or she is a registered Independent.

Please log in or register to add a comment.