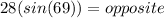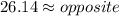Answer:
Explanation:
In this problem, one is given a right triangle, with the length of the hypotenuse given and one of the angles in the triangle. One is asked to find the length of one of the legs. In this situation, one can use right-angle trigonometry. Right angle trigonometry has the following ratios,
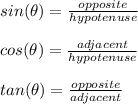
Please note that the sides named (opposite) and (adjacent) are subjective depending on the angle of reference. The side named (hypotenuse) is the side opposite the right angle, its name does not change. In this case, one is given an angle measure and the measurement of the hypotenuse. One is asked to find the length of the side opoosite this angle. One should use the ratio of sine (sin) to achieve this.
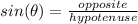
Substitute,
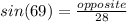
Inverse operations,