What is the constant of variation, k, of the direct variation, y = for, through (5,8)?

Question

asked May 13, 2022 164k views

2 Answers

Mikk Raudsepp · Answer 1 · 2022-05-14T15:49:16+0000

Answer:

8/5

Explanation:

Given that y varies directly with x , therefore ,

$\implies y \propto x$

Let k be the constant . Therefore ,

$\implies y = k x$

When the point is (5,8) ,

$\implies 8 = k * 5 \\\\\implies \underline{\underline{\boxed{ k =(8)/(5)}}}$

Hence the constant of variation is 8/5.

Mathieu Amiot · Answer 2 · 2022-05-20T07:05:51+0000

Answer:

(8)/(5)

Explanation:

The constant of direction variation givens a proportion that is maintained by both x and y values for all points of a line that it passes through.

Usually represented with the variable
, it is given by:

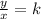(y)/(x)=k for coordinates (x, y).

This relationship can be written as
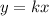y=kx which is also the layout for a proportional relationship.

Since coordinates are written (x, y), for point (5, 8), substitute
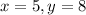x=5, y=8 to get the constant of variation:

$8=5k,\\k=\boxed{(8)/(5)}$