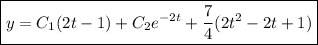Question

Use variation of parameters to find a general solution to the differential equation given that the functions y1 and y2 are linearly independent solutions to the corresponding homogeneous equation for t > 0.

ty'' + (2t - 1)y' - 2y = 7t2 e-2t y1 = 2t - 1, y2 = e-2t

Answer 1

Recall that variation of parameters is used to solve second-order ODEs of the form

y''(t) + p(t) y'(t) + q(t) y(t) = f(t)

so the first thing you need to do is divide both sides of your equation by t :

y'' + (2t - 1)/t y' - 2/t y = 7t

You're looking for a solution of the form

`y=y_1u_1+y_2u_2`

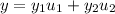
where

`u_1(t)=\displaystyle-\int(y_2(t)f(t))/(W(y_1,y_2))\,\mathrm dt`

`u_2(t)=\displaystyle\int(y_1(t)f(t))/(W(y_1,y_2))\,\mathrm dt`

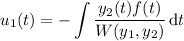
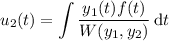
and W denotes the Wronskian determinant.

Compute the Wronskian:

`W(y_1,y_2) = W\left(2t-1,e^(-2t)\right) = \begin{vmatrix}2t-1&e^(-2t)\\2&-2e^(-2t)\end{vmatrix} = -4te^(-2t)`

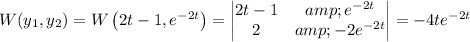
Then

`u_1=\displaystyle-\int(7te^(-2t))/(-4te^(-2t))\,\mathrm dt=\frac74\int\mathrm dt = \frac74t`

`u_2=\displaystyle\int(7t(2t-1))/(-4te^(-2t))\,\mathrm dt=-\frac74\int(2t-1)e^(2t)\,\mathrm dt=-\frac74(t-1)e^(2t)`

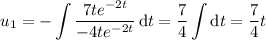
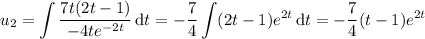
The general solution to the ODE is

`y = C_1(2t-1) + C_2e^(-2t) + \frac74t(2t-1) - \frac74(t-1)e^(2t)e^(-2t)`

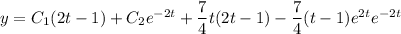
which simplifies somewhat to

`\boxed{y = C_1(2t-1) + C_2e^(-2t) + \frac74(2t^2-2t+1)}`