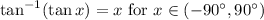Question

Solve for x. Round to the nearest tenth of a degree, if necessary.

Answer 1

`x\approx 49.6^(\circ)`

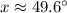
Explanation:

In any right triangle, the tangent of an angle is equal to its opposite side divided by its adjacent side.

For angle
`x`:

• Opposite side is 40
• Adjacent side is 34

Therefore, we have:

`\tan x^(\circ)=(40)/(34)`

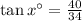
Take the inverse tangent of both sides to solve for
`x`:

`\tan^(-1)(\tan x)=\tan^(-1)((40)/(34)),\\x=\tan^(-1)((40)/(34)),\\x=49.63546343\approx \boxed{49.6^(\circ)}`

*Recall
`\tan^(-1)(\tan x)=x\text{ for } x\in (-90^(\circ), 90^(\circ))`