Answer:
<A ≈ 45 degrees
<B ≈ 57 degrees
<C ≈ 78 degrees
Explanation:
Hi there!
1) Find <C with the law of cosines
Typically, we want to solve for the angle opposite the largest side first.
Law of cosines:
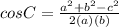
Plug in given values
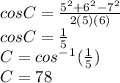
Therefore, <C is approximately 78 degrees.
2) Find <B with the law of cosines

Plug in given values

Therefore, <B is approximately 57 degrees.
3) Find <A
The sum of the interior angles of a triangle is 180 degrees. To solve for <A, subtract <B and <C from 180:
180-57-78
= 45
Therefore, <A is 45 degrees.
I hope this helps!