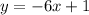Answer:
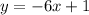
Explanation:
The linear equation with slope m and intercept c is given as follows:
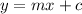
The formula for slope of line with points
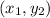 and
and
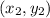 can be expressed as,
can be expressed as,
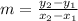
The line passes the points that are
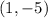 and
and

The slope of the line can be obtained as follows:
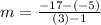
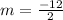
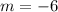
The slope of the line is
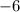
The line passes through the point

Substitute 3 for x, - 6 for m and -17 for y in equation
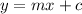 to obtain the value of c.
to obtain the value of c.
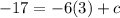

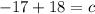
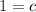
The equation is
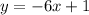
Hence, the equation of the line that passes through the points
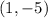 and
and
 is
is