Answer:
(a) The optimum banking Decreases
(b) The optimum banking Increases
(c) The optimum banking is approximately 86.88°
Step-by-step explanation:
(a) The equation of motion on a banked road is given as follows;
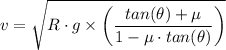
For no friction, we have;
v = √(R·g·tan(θ))
Where;
R₁ = The radius of the road
g = The acceleration due to gravity ≈ 9.81 m/s² = Constant
θ₁ = The bank angle
μ = The coefficient pf friction = Constant
v = The vehicle's speed
If the radius doubles, for no friction, we have;
v² = R·g·(tan(θ))
tan(θ) = v²/(R·g)
Therefore, when the radius doubles, tan(θ) becomes smaller and therefore, the optimum banking angle θ decreases (becomes smaller)
(b) When the speed doubles, we have;
v₁ = 2·v
∴ tan(θ₁) = (v₁)²/(R·g) = 4·(v)²/(R·g) = 4·tan(θ)
When the speed doubles, tan(θ) increases and therefore, the optimum banking angle θ increases increases
(c) The radius negotiated by the car, R = 80 cm = 0.8 m
The speed of the car, v = 12 m/s
From tan(θ) = v²/(R·g), we have;
tan(θ) = 12²/(0.8 × 9.81) ≈ 18.349
θ ≈ arctan(18.349°) ≈ 86.88°