Question

`y = x {}^(2) - 9x + 14`

Given that y can be written in the form

`(x + a) {}^(2) + b`
, where a and b are constants, find the value of a and the value of b.​
pls help i rly need this Pls pls pls pls

Answer 1

a = 4.5

b = -6.25

Explanation:

The given equation to us is ,

`\implies y = x {}^(2) - 9x + 14`

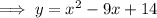
And its given that it can we written in the form of ,

`\implies (x + a) {}^(2) + b`

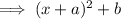
Where ,

• a and b are constants .

Therefore ,

`\implies y = x^2 -9x + 14`

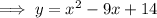
Multiplying 9x by 2/2 ,we have ,

`\implies y = x^2 -(2)/(2)* 9 x + 14`

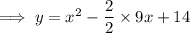
Adding and subtracting (9/2)² ,

`\implies y = \bigg\{ x^2 -(2)/(2)* 9 x + \bigg((9)/(2)\bigg)^2 \bigg\} +14 -\bigg((9)/(2)\bigg)^2`

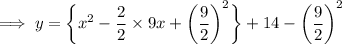
Therefore , we can write it as ,

`\implies y = \bigg( x + (9)/(2)\bigg)^2 + 14 - 20.25 \\\\\implies \underline{\underline{ y = \bigg( x + (9)/(2)\bigg)^2 - 6.25 }}`

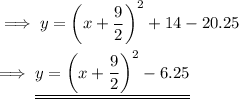
Hence the value of a is 9/2 and b is -6.25 .

Answer 2

a = -
`(9)/(2)` , b = -
`(25)/(4)`

Explanation:

To obtain the required form use the method of completing the square

add/ subtract ( half the coefficient of the x- term)² to x² - 9x

y = x² + 2(-
`(9)/(2)` )x +
`(81)/(4)` -
`(81)/(4)` + 14

= (x -
`(9)/(2)` )² -
`(81)/(4)` +
`(56)/(4)`

= (x -
`(9)/(2)` )²-
`(25)/(4)` ← in the form (x + a)² + b

with a = -
`(9)/(2)` and b = -
`(25)/(4)`