Answer:
Given That:
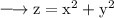
Partial differentiating both sides with respect to x, we get:
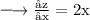
Partial differentiating again with respect to x, we get:
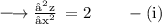
Consider again:
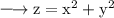
Partial differentiating both sides with respect to y, we get:
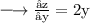
Now, partial differentiating both sides with respect to x, we get:
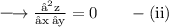
Consider again:
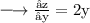
Partial differentiating both sides with respect to y, we get:
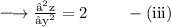
Now, consider Left Hand Side, we get:
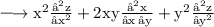
From Equation (i),(ii) and (iii), we can write:
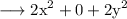
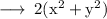
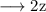
Therefore,
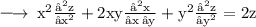
Hence Proved!!

Learn More:-
