Find the value of "a" and "b" for which the limit exists both as x approaches 1 and as x approaches 2:

Question

asked Feb 6, 2022 1.4k views

1 Answer

Afraz · Answer 1 · 2022-02-12T19:13:10+0000

Answer:

a = 4

b = -2

Explanation:

If the given function is continuous at x = 1

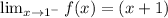
$\lim_(x \to 1^(-)) f(x)=(x+1)$

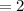
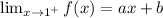
$\lim_(x \to 1^(+)) f(x)=ax+b$

=a+b

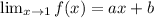
$\lim_(x \to 1) f(x)=ax+b$

=a+b

And for the continuity of the function at x = 1,

$\lim_(x \to 1^(-)) f(x)=\lim_(x \to 1^(+)) f(x)=\lim_(x \to 1) f(x)$

Therefore, (a + b) = 2 -------(1)

If the function 'f' is continuous at x = 2,

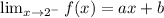
$\lim_(x \to 2^(-)) f(x)=ax+b$

=2a+b

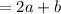
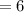
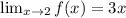
$\lim_(x \to 2^(+)) f(x)=3x$

$\lim_(x \to 2) f(x)=3x$

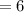
Therefore,
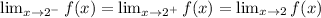
$\lim_(x \to 2^(-)) f(x)=\lim_(x \to 2^(+)) f(x)=\lim_(x \to 2) f(x)$

2a + b = 6 -----(2)

Subtract equation (1) from (2),

(2a + b) - (a + b) = 6 - 2

a = 4

From equation (1),

4 + b = 2

b = -2