Answer:
f(x) has two imaginary roots and one real root.
Explanation:
Complex roots:
I a complex number
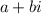 is a root of a polynomial, it's conjugate
is a root of a polynomial, it's conjugate
 is also a root.
is also a root.
One root of a third degree polynomial function f(x) is -5 + 2i.
This means that -5 - 2i is another root of the polynomial, and thus, 2 of the roots are complex.
Third degree, so it has three roots, which means that the third root is real(not possible to have a complex root without it's conjugate), and thus, the correct answer is:
f(x) has two imaginary roots and one real root.