Question

Does it pay to ask for a raise? A national survey of heads of households showed the percentage of those who asked for a raise and the percentage who got one. According to the survey, of the men interviewed, 21% had asked for a raise and 60% of the men who had asked for a raise received the raise. If a man is selected at random from the survey population of men, find the following probabilities. (Enter your answers to three decimal places.)

Answer 1

a) P(man asked for a raise) = 0.21.

b) P(man received raise, given he asked for one) = 0.6.

c) P(man asked for raise and received raise) = 0.126.

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

Question a:

21% asked for a raise, so:

P(man asked for a raise) = 0.21.

Question b:

Event A: Asked for a raise.

Event B: Received a raise:

21% had asked for a raise and 60% of the men who had asked for a raise received the raise:

This means that
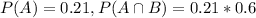`P(A) = 0.21, P(A \cap B) = 0.21*0.6`, thus:

`P(B|A) = (P(A \cap B))/(P(A)) = (0.21*0.6)/(0.6) = 0.6`

P(man received raise, given he asked for one) = 0.6.

Question c:

`P(A \cap B) = 0.21*0.6 = 0.126`

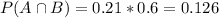
P(man asked for raise and received raise) = 0.126.