Answer:
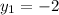 and
and
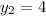
Explanation:
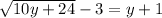
Move the constant to the right-hand side and change their sign.
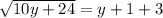
combine like terms
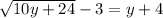
Square both side to remove square brackets.
10y + 24 - 3 = y²+ 8y + 16
Move the expression to the left-hand side and change its sign.
10y + 24 - y² - 8y - 16 = 0
Combine like terms
10y - 8y + 24 - 16 - y² = 0
2y + 8 - y² = 0
Use commutative property to reorder the terms.
-y² + 2y + 8 = 0
Change the sign of expression.
y² -2y -8 = 0
split -2y
y² + 2y - 4y - 8 = 0
Factor out y from the first pair and -4 from the second equation.
y ( y + 2 ) - 4 ( y + 2 ) = 0
Factor out y+2 from the expression.
( y + 2 ) ( y - 4)
When the products and factors equals 0, at least one factor is 0.
y + 2 = 0
y - 4 = 0
Solve for y
y = -2
y = 4
When we plug the both solution as y we found that both is true solution of this equation.
This equation has two solutions which are -2 and 4.