Answer: Choice D. (2, -1)
======================================================
Step-by-step explanation:
Double everything in the second equation to go from x-y = 3 to 2x-2y = 6.
So we have this equivalent system of equations
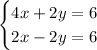
We can then add straight down. The x terms add to 6x. The y terms go away because they add to 0. The stuff on the right hand sides add to 12.
After those three sets of addition operations, we have the new equation 6x = 12 which solves to x = 2 after dividing both sides by 6.
Now use x = 2 with any of the equations mentioned that have x,y involved so we can solve for y.
4x+2y = 6
4(2)+2y = 6
8+2y = 6
2y = 6-8
2y = -2
y = -2/2
y = -1
or we could say
x-y = 3
2-y = 3
-y = 3-2
-y = 1
y = -1
Either way, we get the same y value.
Since x = 2 and y = -1 pair up together, we get the ordered pair solution (x,y) = (2, -1). Therefore, the answer is choice D.
If you were to graph the two equations, as shown below, the two lines intersect at (2,-1). This point is on both lines at the same time. This is visual confirmation that the point is a solution to both equations. Though you should still algebraically check each original equation.