Answer:
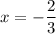
Explanation:
We want to solve the equation:
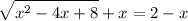
We can isolate the square root. Subtract x from both sides:
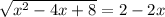
And square both sides:
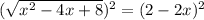
Expand:
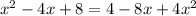
Isolate the equation:
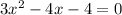
Factor:
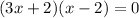
Zero Product Property:
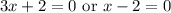
Solve for each case. Hence:

Now, we need to check for extraneous solutions. To do so, we can substitute each value back into the original equation and check whether or not the resulting statement is true.
Testing x = -2/3:

Since the resulting statement is true, x = -2/3 is indeed a solution.
Testing x = 2:
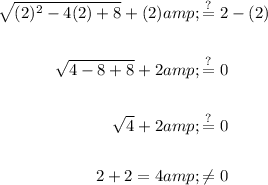
Since the resulting statement is not true, x = 2 is not a solution.
Therefore, our only solution to the equation is x = -2/3.