Solve with explanation please

Question

asked Nov 19, 2023 2.0k views

1 Answer

Erc · Answer 1 · 2023-11-23T21:43:47+0000

Answer:

Length of the rectangular lot = 60 meters

Width of the rectangular lot = 30 meters

Explanation:

Let the width of the rectangular lot be x meters.

So, Length of the same = 2x metres.

$A(rectangular \:lot) = (2x)(x)$

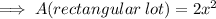
$\implies A(rectangular \:lot) = 2x^2$

When length is increasEd by 40 m and width by 6 m. Then....

New length =
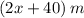
$(2x + 40) \:m$

New width =
$(x + 6) \:m$

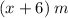
According to the question:

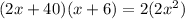
(2x + 40)(x + 6) = 2(2x^2)

$\implies 2x(x + 6) + 40(x + 6) - 4x^2=0$

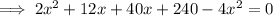
$\implies 2x^2+12x + 40x + 240 - 4x^2=0$

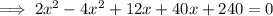
$\implies 2x^2- 4x^2+12x + 40x + 240 =0$

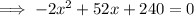
$\implies -2x^2+52x + 240 =0$

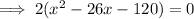
$\implies 2(x^2-26x - 120) =0$

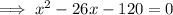
$\implies x^2-26x - 120=0$

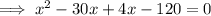
$\implies x^2-30x+4x - 120=0$

$\implies x(x-30)+4(x - 30)=0$

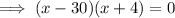
$\implies (x-30)(x+4)=0$

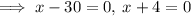
$\implies x-30=0,\: x+4=0$

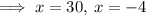
$\implies x=30,\: x=-4$

Since, x represents the side length, so its value can't be negative.

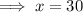
$\implies x=30$

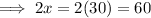
$\implies 2x=2(30)=60$

Thus,

Length of the rectangular lot = 60 meters

Width of the rectangular lot = 30 meters