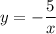Question

NO LINKS OR ANSWERING WHAT YOU DON'T KNOW!!!!!

7. Suppose y varies inversely with x, and y = 39 when x = 1/3. What is the value of y when x = 26.
a. 3
b. 2
c. 1/2
d. 13

8. Suppose y varies inversely with x, and y = 25 when x = -1/5. What inverse variation equation relates x and y?
a. y = 5/x
b. y = -5/x
c. y = 5x
d. y= -5x

Answer 1

Problem 7) C

Problem 8) B

Explanation:

Recall that inverse variation has the form:

`\displaystyle y=(k)/(x)`

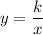
Where k is the constant of variation.

Problem 7)

We are given that y = 39 when x = 1/3. Thus:

`\displaystyle 39=\frac{k}{{}^(1)\!/ \!{}_(3)}`

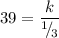
Solve for k:

`\displaystyle k=(1)/(3)(39)=13`

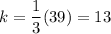
Hence, our equation is:

`\displaystyle y=(13)/(x)`

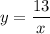
Then when x = 26, y equals:

`\displaystyle y=(13)/((26))=(1)/(2)`

Problem 8)

We are given that y = 25 when x = -1/5. Thus:

`\displaystyle 25=\frac{k}{-{}^(1)\!/ \!{}_(5)}`

Solve for k:

`\displaystyle k=-(1)/(5)(25)=-5`

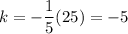
Hence, our equation is:

`\displaystyle y=-(5)/(x)`