Answer:
The value of teh test statistic is
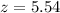
The p-value of the test is 0 < 0.05, which means that there is significant evidence to conclude that the proportion differs from 0.2.
Explanation:
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
0.2 is tested at the null hypothesis:
This means that
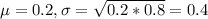
Using the sample results p^=0.27 with n=1003
This means that

Value of the test statistic:

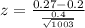
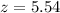
P-value of the test and decision:
The p-value of the test is the probability that the sample proportion differs from 0.2 by at least 0.07, which is P(|z| > 5.54), that is, 2 multiplied by the p-value of z = -5.54.
Looking at the z-table, z = -5.54 has a p-value of 0.
2*0 = 0.
The p-value of the test is 0 < 0.05, which means that there is significant evidence to conclude that the proportion differs from 0.2.