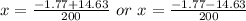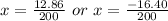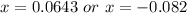Answer:
When this equation is solved, the two values of the unknown are 0.0643 and -0.082
Step-by-step explanation:
Given
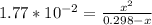 --- the actual equation
--- the actual equation
Required
The values of x
We have:
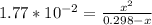
Cross Multiply
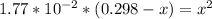
Multiply both sides by 100
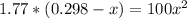
Open bracket
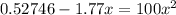
Rewrite as:
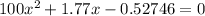
Using quadratic formula:
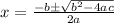
Where:
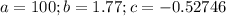
So, we have:


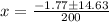
Split