Question

A 64-ka base runner begins his slide into second base when he is moving at a speed of 3.2 m/s. The coefficient of friction between his clothes and Earth is 0.70. He slides so that his speed is zero just as he reaches the base.

Required:
a. How much mechanical energy is tout due to friction acting on the runner?
b, How far does he slide?

Answer 1

Step-by-step explanation:

From the given information:

mass = 64 kg

speed = 3.2 m/s

coefficient of friction
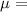`\mu =` 0.70

The mechanical energy touted relates to the loss of energy in the system as a result of friction and this can be computed as:

`W = \Delta K.E`

`\implies (1)/(2)m(v^2 -u^2)`

`= (1)/(2)(64.0 \kg) (0 - (3.2 \ m/s^2))`

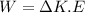
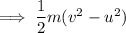
Thus, the mechanical energy touted = 327.68 J

According to the formula used in calculating the frictional force

`F_r = \mu mg`

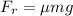
= 0.70 × 64 kg× 9.8 m/s²

= 439.04 N

The distance covered now can be determined as follows:

d = W/F

d = 327.68 J/ 439.04 N

d = 0.746 m