Answer:
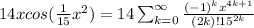
Explanation:
In order to find this Maclaurin series, we can start by using a known Maclaurin series and modify it according to our function. A pretty regular Maclaurin series is the cos series, where:

So all we need to do is include the additional modifications to the series, for example, the angle of our current function is:
 so for
so for

the modified series will look like this:
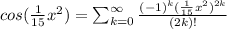
So we can use some algebra to simplify the series:
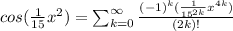
which can be rewritten like this:
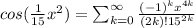
So finally, we can multiply a 14x to the series so we get:

We can input the x into the series by using power rules so we get:
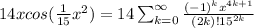
And that will be our answer.