Answer:
$55.4930
Step-by-step explanation:
Use the following formula to calculate the value of the call option
Value of call option = (
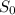 x N(
x N(
 ) ) - (K x
) ) - (K x
 x N(
x N(
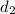 ))
))
where
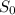 = current spot price = $200
= current spot price = $200
K = strike price = $180
r = risk-free interest rate
t is the time to expiry in years
N (
 ) = NORMSDIST [ (ln(S0 / K) + (r + σ2/2) x T) / σ√T ] = NORMSDIST [ ln(200 / 180) + (0.21 + (0.2252/2) x 1 / 0.225 x √1 ] = 0.9350
) = NORMSDIST [ (ln(S0 / K) + (r + σ2/2) x T) / σ√T ] = NORMSDIST [ ln(200 / 180) + (0.21 + (0.2252/2) x 1 / 0.225 x √1 ] = 0.9350
N (
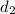 ) = NORMSDIST [d1 - σ√T ] = NORMSDIST [ 0.9350 - 0.225 x √1 ] = 0.9013
) = NORMSDIST [d1 - σ√T ] = NORMSDIST [ 0.9350 - 0.225 x √1 ] = 0.9013
Placing values in the formula
Value of call option = ( $200 x 0.9350 ) - ($180 x
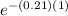 x 0.9013)
x 0.9013)
Value of call option = $55.4930