Question

Suppose speeds of vehicles traveling on a highway have an unknown distribution with mean 63 and standard deviation 4 miles per hour. A sample of size n-44 is randomly taken from the population and the mean is taken. Using the Central Limit Theorem for Means, what is the standard deviation for the sample mean distribution?

Answer 1

The standard deviation for the sample mean distribution=0.603

Explanation:

We are given that

Mean,
`\mu=63`

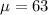
Standard deviation,
`\sigma=4`

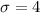
n=44

We have to find the standard deviation for the sample mean distribution using Central Limit Theorem for Means.

Standard deviation for the sample mean distribution

`\sigma_x=(\sigma)/(√(n))`

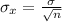
Using the formula

`\sigma_x=(4)/(√(44))`

`\sigma_x=(4)/(√(2* 2* 11))`

`\sigma_x=(4)/(2√(11))`

`\sigma_x=(2)/(√(11))`

`\sigma_x=0.603`

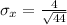
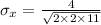
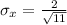
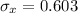
Hence, the standard deviation for the sample mean distribution=0.603