Answer:
Following are the solution to the given question:
Explanation:
Performance of the student's t-test as

n<30
Calculating the Null hypothesis:
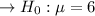
Calculating the Alternative Hypothesis:

Calculating the level of significance
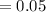
Calculating the test statistic:

Because of the population standard deviation, perform z test
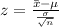
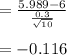
Decision:
Comparison of p-value test statistics and decision-making.
Hypothesis P<0.05 Reject.
P>0.05 No hypothesis rejecting zero.
P-Value = 0.907653.
At p<0.05 the result is not significant.
Null hypothesis not to be rejected.
Accepting the null hypothesis.
Conclusion:
Its assertion that the containers were not refilled appropriately by the specified amount of 6 ounces/bottle doesn't contain substantial proof. Bottles with mean = 6 ounces are suitably filled.