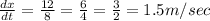Answer:
Explanation:
This is a related rates problem from calculus using implicit differentiation. The main equation is Pythagorean's Theorem. Basically, what we are looking for is
 when y = 6 and
when y = 6 and
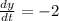 .
.
The equation for Pythagorean's Theorem is
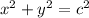 where x and y are the legs and c is the hypotenuse. The length of the hypotenuse is 10, so when we find the derivative of this function with respect to time, and using implicit differentiation, we get:
where x and y are the legs and c is the hypotenuse. The length of the hypotenuse is 10, so when we find the derivative of this function with respect to time, and using implicit differentiation, we get:
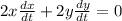 and divide everything by 2 to simplify:
and divide everything by 2 to simplify:
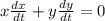 . Looking at that equation, it looks like we need a value for x, y,
. Looking at that equation, it looks like we need a value for x, y,
 and
and
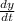 .
.
Since we are looking for
 , that can be our only unknown and everything else has to have a value. So what do we know?
, that can be our only unknown and everything else has to have a value. So what do we know?
If we construct a right triangle with 10 as the hypotenuse and use 6 for y, we can solve for x (which is the only unknown we have, actually). Using Pythagorean's Theorem to solve for x:
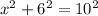 and
and
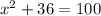 and
and
 so
so
x = 8.
NOW we can fill in the derivative and solve for
 .
.
Remember the derivative is
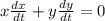 so
so
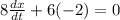 and
and
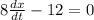 and
and
 so
so