Question

If the range of the coordinate transformation (, ) = (−2,−3 +1) is (4, −2), (2, −5), (−6, 4), what is the domain?

A. (-2, 1), (-1, 2), (3, -1)

B. (-8, 7), (-4, 16), (19, -11)

C. (-8, 1), (-4, 2), (19, -1)

D. (-2, 7), (-1, 16), (3, -11)

Answer 1

Consider the below figure attached with this question.

Given:

The transformation is:

`f(x,y)=(-2x,-3y+1)`

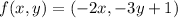
The range is (4,-2), (2, −5), (−6, 4).

To find:

The domain of the transformation.

Solution:

We have,

`f(x,y)=(-2x,-3y+1)`

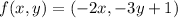
For the point (4,-2),

`(-2x,-3y+1)=(4,-2)`

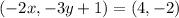
On comparing both sides, we get

`-2x=4`

`x=(4)/(-2)`

`x=-2`

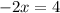
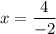
And,

`-3y+1=-2`

`-3y=-2-1`

`-3y=-3`

`y=(-3)/(-3)`

`y=1`

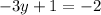
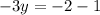
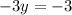
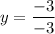
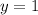
So, the domain of (4,-2) is (-2,1).

Similarly,

For the point (2,-5),

`(-2x,-3y+1)=(2,-5)`

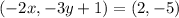
On comparing both sides, we get
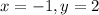`x=-1,y=2`. So, the domain of (2,-5) is (-1,2).

For the point (-6,4),

`(-2x,-3y+1)=(-6,4)`

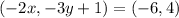
On comparing both sides, we get
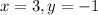`x=3,y=-1`. So, the domain of (-6,4) is (3,-1).

So, the domain of the given transformation is (-2, 1), (-1, 2), (3, -1).

Therefore, the correct option is A.