Given:
The three exterior angles of a pentagon measures 60,80 and 90.
To find:
The measure of other two exterior angle, assuming them equally.
Solution:
Let x be the measure of two other exterior angles of the pentagon.
We know that the sum of all exterior angles of a pentagon is 360 degrees.

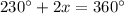
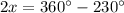

Divide both sides by 2.

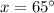
Therefore, the measures of both exterior angles are 65 degrees.