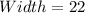Answer:
See attachment for graph
The height of the arch is: 120 m
The width to the nearest meter, at the base of the arch is 22 m
Explanation:
Given
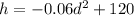
Solving (a): The graph
See attachment for graph
Variable h is plotted on the vertical axis while variable d is plotted on the horizontal axis.
Solving (b): The height
The curve of
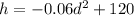 opens downward. So, the maximum point on the vertical axis represents the height of the arch,
opens downward. So, the maximum point on the vertical axis represents the height of the arch,
Hence:
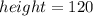
Solving (c): The width
The curve touches the horizontal axis at two different points.
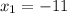
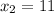
The absolute difference of both points represents the width.
So:
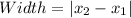
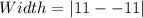
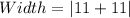
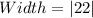
Hence: