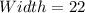Question

An arch is in the form of a parabola given by the function h = -0.06d^2 + 120, where the origin is at ground level, d meters is the horizontal distance and h is the height of the arch in meters.

Graph this function on your graphing calculator then complete the following statements.
The height of the arch is: ------- m
The width to the nearest meter, at the base of the arch is ------ m

Answer 1

See attachment for graph

The height of the arch is: 120 m

The width to the nearest meter, at the base of the arch is 22 m

Explanation:

Given

`h = -0.06d^2 + 120`

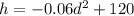
Solving (a): The graph

See attachment for graph

Variable h is plotted on the vertical axis while variable d is plotted on the horizontal axis.

Solving (b): The height

The curve of
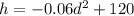`h = -0.06d^2 + 120` opens downward. So, the maximum point on the vertical axis represents the height of the arch,

Hence:

`height = 120`

Solving (c): The width

The curve touches the horizontal axis at two different points.

`x_1 = -11`

`x_2 = 11`

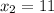
The absolute difference of both points represents the width.

So:

`Width = |x_2 - x_1|`

`Width = |11 - -11|`

`Width = |11 +11|`

`Width = |22|`

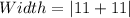
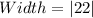
Hence:

`Width = 22`