Question

A normal distribution has \mu = 65 and \sigma = 10. Find the probability that the average score of a group of n = 4 people is between 70 and 75 (both limits included).

Answer 1

The probability that the average score of a group of n = 4 people is between 70 and 75=0.13591

Explanation:

We are given that

`\mu=65`

`\sigma=10`

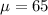
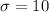
n=4

We have to find the probability that the average score of a group of n = 4 people is between 70 and 75.

`P(70<\bar{x}<75)=P((70-65)/((10)/(√(4)))<\frac{\bar{x}-\mu}{(\sigma)/(√(n))}<(75-65)/((10)/(√(4))))`

`=P((5)/(5)<Z<(10)/(5))`

`=P(1<Z<2)`

`=P(Z<2)-P(Z<1)`

`=0.97725-0.84134`

`=0.13591`

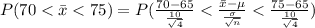
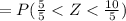
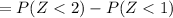
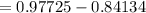
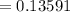
Hence, the probability that the average score of a group of n = 4 people is between 70 and 75=0.13591