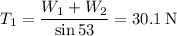1 Answer

Shrikant K · Answer 1 · 2022-03-03T12:15:50+0000

30.1 N

Step-by-step explanation:

Given:

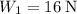
$W_1 = 16\:\text{N}$

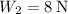
$W_2 = 8\:\text{N}$

Let's write the components of the net forces at the intersections. Note that the system is equilibrium so all the net forces are zero.

Forces involving W1:

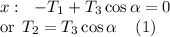
$x:\:\:\:-T_1 + T_3\cos \alpha = 0\:\: \\ \text{or}\:\:T_2 = T_3\cos \alpha\:\:\:\:\:(1)$

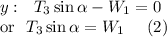
$y:\:\:\:T_3\sin \alpha - W_1 = 0\:\:\: \\ \text{or}\:\:\:T_3\sin \alpha = W_1\:\:\:\:\:\:(2)$

Forces involving W2:

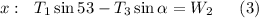
$x:\:\:\:T_1\sin 53 - T_3\sin \alpha = W_2\:\:\:\:\:\:\:(3)$

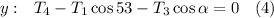
$y:\:\:\:T_4 - T_1\cos 53 - T_3\cos \alpha = 0\:\:\:\;(4)$

Substitute (2) into (3) and we get

$T_1\sin 53 - W_1 = W_2$

Solving for
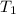T_1 ,

$T_1 = (W_1 + W_2)/(\sin 53) = 30.1\:\text{N}$

Please log in or register to add a comment.