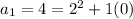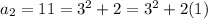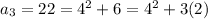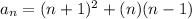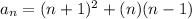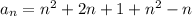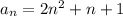Answer:
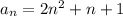
Explanation:
4, 11, 22, 37, 56
11 - 4 = 7
22 - 11 = 11
37 - 22 = 15
56 - 37 = 19
After the first difference, 11 - 4 = 7, each difference is 4 more than the previous difference.
Difference of differences:
11 - 7 = 4
15 - 11 = 4
19 - 15 = 4
Since we need the difference of differences to find a constant, this must be a second degree function.