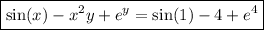(3.1) … … …
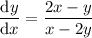
Multiply the right side by x/x :
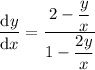
Substitute y(x) = x v(x), so that dy/dx = x dv/dx + v :
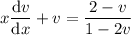
This DE is now separable. With some simplification, you get
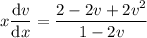
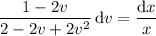
Now you're ready to integrate both sides (on the left, the denominator makes for a smooth substitution), which gives
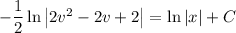
Solve for v, then for y (or leave the solution in implicit form):
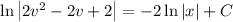
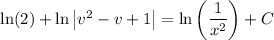
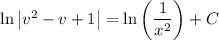
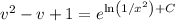
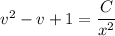
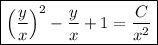
(3.2) … … …
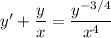
It may help to recognize this as a Bernoulli equation. Multiply both sides by
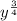 :
:
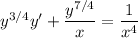
Substitute
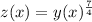 , so that
, so that
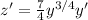 . Then you get a linear equation in z, which I write here in standard form:
. Then you get a linear equation in z, which I write here in standard form:
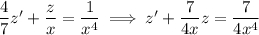
Multiply both sides by an integrating factor,
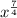 , which gives
, which gives
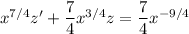
and lets us condense the left side into the derivative of a product,
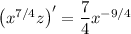
Integrate both sides:
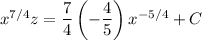
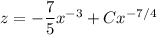
Solve in terms of y :
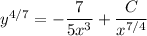
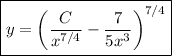
(3.3) … … …
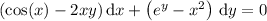
This DE is exact, since
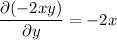
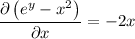
are the same. Then the general solution is a function f(x, y) = C, such that
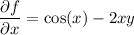
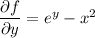
Integrating both sides of the first equation with respect to x gives
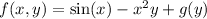
Differentiating this result with respect to y then gives
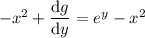
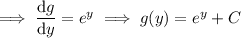
Then the general solution is
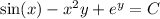
Given that y (1) = 4, we find
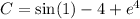
so that the particular solution is