Answer:
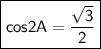
Explanation:
Here we are given that the value of sinA is √3-1/2√2 , and we need to prove that the value of cos2A is √3/2 .
Given :-
•
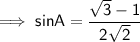
To Prove :-
•

Proof :-
We know that ,
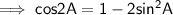
Therefore , here substituting the value of sinA , we have ,
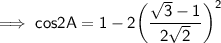
Simplify the whole square ,
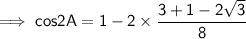
Add the numbers in numerator ,
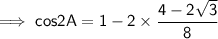
Multiply it by 2 ,
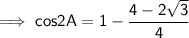
Take out 2 common from the numerator ,
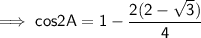
Simplify ,
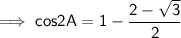
Subtract the numbers ,
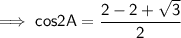
Simplify,
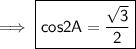
Hence Proved !