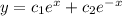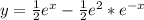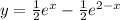Question

family of solutions of the second-order DE y y 0. Find a solution of the second-order IVP consisting of this differential equation and the given initial conditions. 12. y(1) 0, y(1) e

Answer 1

`y = (1)/(2)e^x -(1)/(2) e^(2-x)`

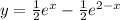
Explanation:

Given

`y=c_1e^x +c_2e^{-x`

`y(1) = 0`

`y'(1) =e`

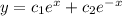
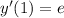
Required

The solution

Differentiate
`y=c_1e^x +c_2e^{-x`

`y' = c_1e^x - c_2e^(-x)`

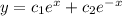
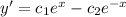
Next, we solve for c1 and c2

`y(1) = 0` implies that; x = 1 and y = 0

So, we have:

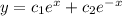
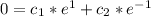
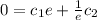`y=c_1e^x +c_2e^{-x`

`0 = c_1 * e^1 + c_2 * e^(-1)`

`0 = c_1 e + (1)/(e)c_2` --- (1)

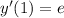`y'(1) =e` implies that: x = 1 and y' = e

So, we have:

`y' = c_1e^x - c_2e^(-x)`

`e = c_1 * e^1 - c_2 * e^(-1)`

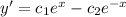
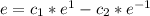
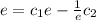`e = c_1 e - (1)/(e)c_2` --- (2)

Add (1) and (2)

`0 + e = c_1e + c_1e + (1)/(e)c_2 - (1)/(e)c_2`

`e = 2c_1e`

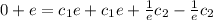
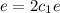
Divide both sided by e

`1 = 2c_1`

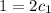
Divide both sides by 2

`c_1 = (1)/(2)`

Substitute
`c_1 = (1)/(2)` in
`0 = c_1 e + (1)/(e)c_2`

`0 = (1)/(2) e+ (1)/(e)c_2`

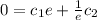
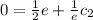
Rewrite as:

`(1)/(e)c_2 = -(1)/(2) e`

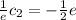
Multiply both sides by e

`c_2 = -(1)/(2) e^2`

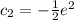
So, we have:

`y=c_1e^x +c_2e^{-x`

`y = (1)/(2)e^x -(1)/(2) e^2 * e^(-x)`

`y = (1)/(2)e^x -(1)/(2) e^(2-x)`