Question

The width of a rectangle is only 15% of its length. If the perimeter of the rectangle is 46, what is the length

Answer 1

20 units

Explanation:

Let the length be x. According to the question,

• Length = x
• Width = 15% of the length

➝ Width = 15% of the length

➝ Width = 15/100x

➝ Width = 3/20x

We have the perimeter of the rectangle that is 46 units.

`\longrightarrow \sf {Perimeter_((Rec.)) = 2(L + W) } \\`

`\longrightarrow \sf {46= 2\Bigg \lgroup x + (3)/(20)x \Bigg \rgroup } \\`

`\longrightarrow \sf {46= 2\Bigg \lgroup x + (3)/(20)x \Bigg \rgroup } \\`

`\longrightarrow \sf {46= 2\Bigg \lgroup (20x + 3x)/(20) \Bigg \rgroup } \\`

`\longrightarrow \sf {46= 2\Bigg \lgroup (23x)/(20) \Bigg \rgroup } \\`

`\longrightarrow \sf {(46)/(2)= (23x)/(20)} \\`

`\longrightarrow \sf {23= (23x)/(20)} \\`

`\longrightarrow \sf {23 * 20 = 23x} \\`

`\longrightarrow \sf {460= 23x} \\`

`\longrightarrow \sf {\cancel{(460)/(23)} = x} \\`

`\longrightarrow \underline{\boxed{ \bf {20\; units = x}}} \\`

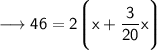
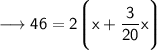
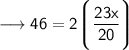
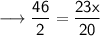
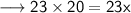
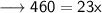
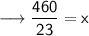
Therefore, length of the rectangle is 20 units.