Answer:
B) 67°C.
Explanation:
Newton's Law of Cooling is given by:
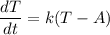
Where T is the temperature of the coffee, A is the room temperature, and k is a positive constant.
We are given that the coffee cools from 100°C to 90°C in one minute at a room temperature A of 25°C.
And we want to find the temperature of the coffee after four minutes.
First, solve the differential equation. Multiply both sides by dt and divide both sides by (T - A). Hence:
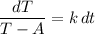
Take the integral of both sides:
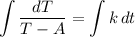
Integrate:
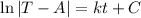
Raise both sides to e:
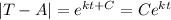
The temperature of the coffee T will always be greater than or equal to the room temperature A. Thus, we can remove the absolute value:
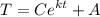
We are given that A = 25. Hence:
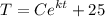
Since the coffee cools from 100°C to 90°C, the initial temperature of the coffee was 100°C. Thus, when t = 0,T = 100:

Hence:
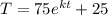
We are given that the coffee cools from 100°C to 90°C after one minute at a room temperature of 25°C.
So, T = 90 given that t = 1. Substitute:
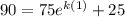
Solve for k:
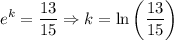
Therefore:
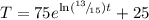
Then after four minutes, the temperature of the coffee will be:
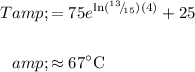
Hence, our answer is B.