Question

Solve the logarithmic equation

`log_(6)(2x - 6) + log_(6)x = 2`
​

Answer 1

x = 6

Explanation:

The given logarithmic equation is ,

`\implies log_(6)(2x - 6) + log_(6)x = 2`

We can notice that the bases of both logarithm is same . So we can use a property of log as ,

`\bf \to log_a b + log_a c = log_a {( ac)}`

So we can simplify the LHS and write it as ,

`\implies log_(6) \{ x ( 2x - 6 )\} = 2`

Now simplify out x(2x - 6 ) . We get ,

`\implies log_6 ( 2x^2 - 6x ) = 2`

Again , we know that ,

`\bf \to log_a b = c , a^c = b`

Using this we have ,

`\implies 2x^2 - 6x = 6^2 \\\\\implies 2x^2 - 6x -36 = 0`

Now simplify the quadratic equation ,

`\implies x^2 - 3x - 18 = 0 \\\\\implies x^2 -6x + 3x -18=0\\\\\implies x( x -6) +3( x - 6 ) = 0 \\\\\implies (x-6)(x+3) = 0 \\\\\implies x = 6 , -3`

Since logarithms are not defined for negative numbers or zero , therefore ,

`\implies 2x - 6 > 0 \\\\\implies x > 3`

Therefore the equation is not defined at x = -3 . Hence the possible value of x is 6 .

`\implies \underline{\underline{ x \quad = \quad 6 }}`

Answer 2

`x=6`

Explanation:

We want to solve the equation:

`\displaystyle \log_6(2x-6)+\log_6x=2`

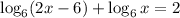
Recall the property:

`\displaystyle \log_bx+\log_by=\log_b(xy)`

Hence:

`\log_6(x(2x-6))=2`

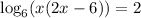
Next, recall that by the definition of logarithms:

`\displaystyle \log_b(a)=c\text{ if and only if } b^c=a`

Therefore:

`6^2=x(2x-6)`

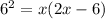
Solve for x. Simplify and distribute:

`36=2x^2-6x`

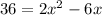
We can divide both sides by two:

`x^2-3x=18`

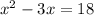
Subtract 18 from both sides:

`x^2-3x-18=0`

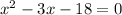
Factor:

`(x-6)(x+3)=0`

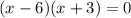
Zero Product Property:

`x-6=0\text{ or } x+3=0`

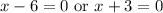
Solve for each case. Hence:

`x=6\text{ or } x=-3`

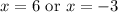
Next, we must check the solutions for extraneous solutions. To do so, we can simply substitute the solutions back into the original equations and examine its validity.

Checking x = 6:

`\displaystyle \begin{aligned} \log_(6)(2(6)-6)+\log_(6)6&\stackrel{?}{=} 2 \\ \\ \log_6(12-6)+(1)&\stackrel{?}{=}2 \\ \\ \log_6(6)+1&\stackrel{?}{=}2 \\ \\ 1+1=2&\stackrel{\checkmark}{=}2\end{aligned}`

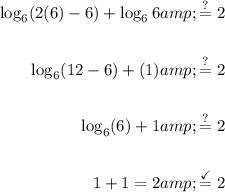
Hence, x = 6 is indeed a solution.

Checking x = -3:

`\displaystyle\begin{aligned} \log_6(2(-3)-6) + \underbrace{\log_6-3}_{\text{und.}} &\stackrel{?}{=} 2\\ \\ \end{aligned}`

Since the second term is undefined, x = -3 is not a solution.

Therefore, our only solution is x = 6.