9514 1404 393
Answer:
0.5
Explanation:
The "enclosed area" can be taken to mean different things. Here, we consider it to mean the finite area bounded between the two curves, regardless of which curve is higher value than the other.
The area is bounded on the interval [0, 2]. On half that interval y1 > y2; on the other half, y2 > y1. This means the integral of the area between the curves will be different for one part of the interval than for the other. (The curves are symmetric about the point (1, 0).)
The area on the interval [0, 1] is given by the integral ...
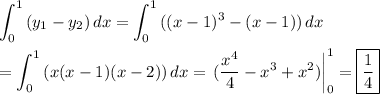
The area on the interval [1, 2] is the integral of the opposite integrand, but has the same value.
The positive area over the whole interval from 0 to 2 is 1/4+1/4 = 1/2.
If you simply integrate y2-y1 or y1-y2 over that interval, the result is 0.