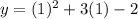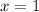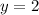Answer:
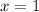
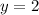
Explanation:
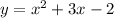 ,
,
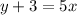
Replace all occurrences of
 in
in
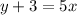 with
with
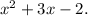

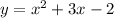
Add
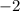 and 3.
and 3.
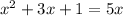
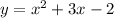
Subtract 5x from both sides of the equation.
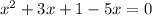
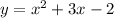
Subtract 5x from 3x.
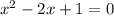
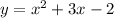
Rewrite 1 as
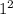 .
.
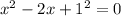
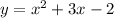
Check that the middle term is two times the product of the numbers being squared in the first term and third term.
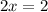 ·
·
 ·
·

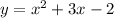
Rewrite the polynomial.
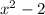 ·
·
 ·
·



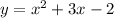
Factor using the perfect square
trinomial rule
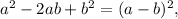
where a = x and b = 1.

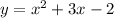
Set the
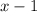 equal to 0.
equal to 0.
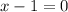
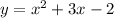
Add 1 to both sides of the equation.
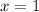
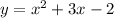
Replace all occurrences of
 in
in
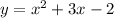 with 1.
with 1.