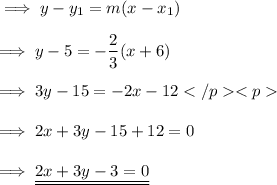Question

PLEASE HELP!!! What is the equation of the line perpendicular to 2x – 3y = 13 that passes through the point (–6, 5)?

Answer 1

y = -
`(3)/(2)`x - 4

Explanation:

2x – 3y = 13

3y = 2x + 13

y =
`(2)/(3)`x +
`(13)/(3)`

slope = 2/3

negative reciprocal = -3/2

y = -3/2x + b

(-6, 5)

5 = (-3/2)(-6) + b

5 = 9 + b

b = -4

y = -3/2x - 4

Answer 2

2x + 3y -3=0

Explanation:

The given equation of the line is ,

`\implies 2x - 3y = 13`

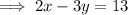
Now convert it into slope intercept form to get the slope , we get ,

`\implies 3y = 2x - 13 \\\\\implies y =(2)/(3)x -(13)/(2)`

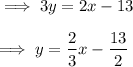
Therefore the slope is ,

`\implies m = (2)/(3)`

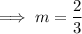
We know that the product of slope of perpendicular lines is -1 . Therefore the slope of the perpendicular line will be ,

`\implies m_(perpendicular)= -(2)/(3)`

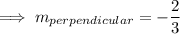
Now one of the point is (-6,5) .On Using point slope form , we have ,

`\implies y-y_1 = m( x - x_1) \\\\\implies y - 5 = -(2)/(3)( x + 6 ) \\\\\implies 3y - 15 = -2x -12 </p><p>\\\\\implies 2x + 3y -15+12=0 \\\\\implies \underline{\underline{ 2x + 3y -3=0 }}`