Answer:
The surface gravity g of the planet is 1/4 of the surface gravity on earth.
Step-by-step explanation:
Surface gravity is given by the following formula:
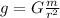
So the gravity of both the earth and the planet is written in terms of their own radius, so we get:
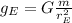
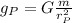
The problem tells us the radius of the planet is twice that of the radius on earth, so:
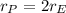
If we substituted that into the gravity of the planet equation we would end up with the following formula:
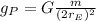
Which yields:
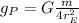
So we can now compare the two gravities:
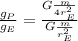
When simplifying the ratio we end up with:
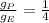
So the gravity acceleration on the surface of the planet is 1/4 of that on the surface of Earth.