Question

The weights of certain machine components are normally distributed with a mean of 8.04 g and a standard deviation of 0.08 g. Find the two weights that separate the top 3% and the bottom 3%. (These weights could serve as limits used to identify which components should be rejected)

Answer 1

The bottom 3 is separated by weight 7.8896 g and the top 3 is separated by weight 8.1904 g.

Explanation:

We are given that

Mean,
`\mu=8.04 g`

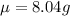
Standard deviation,
`\sigma=0.08g`

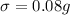
We have to find the two weights that separate the top 3% and the bottom 3%.

Let x be the weight of machine components

`P(X<x_1)=0.03, P(X>x_2)=0.03`

`P(X<x_1)=P(Z<(x_1-8.04)/(0.08))`

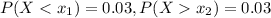
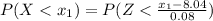
=0.03

From z- table we get

`P(Z<-1.88)=0.03, P(Z>1.88)=0.03`

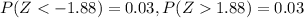
Therefore, we get

`(x_1-8.04)/(0.08)=-1.88`

`x_1-8.04=-1.88* 0.08`

`x_1=-1.88* 0.08+8.04`

`x_1=7.8896`

`(x_2-8.04)/(0.08)=1.88`

`x_2=1.88* 0.08+8.04`

`x_2=8.1904`

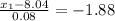
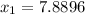
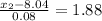
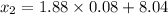
Hence, the bottom 3 is separated by weight 7.8896 g and the top 3 is separated by weight 8.1904 g.