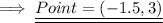Explanation:
The two equation will intersect each other at the point which will be the solution of the given two equations , and the given equations are ,
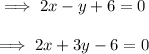
On subtracting the given equations we have,

Put this value in any equation , we have ,
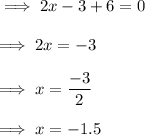
Hence the lines will Intersect at ,