Answer:
Explanation:
If the product of 2 integers is -12, then that equation looks like this:
xy = -12
If the sum of those same 2 integers in 1, then that equation looks like this:
x + y = 1
Let's solve the second equation for x and plug it into the first equation. Solving the second equation for x gives us
x = 1 - y and plug that into the first equation in place of x to get:
(1 - y)y = -12 and
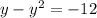 Now move everything over to one side and factor to find y:
Now move everything over to one side and factor to find y:
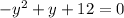 and the 2 values for y are
and the 2 values for y are
y = -3 and y = 4. Let's see what happens when we solve for x.
If xy = -12 and y is -3:
x(-3) = -12 so
x = 4
If xy = -12 and y is4:
x(4) = -12 so
x = -3
So it looks like the 2 integers are -3 and 4