inside the circle
Explanation:
we want to verify whether (-4,2) lies inside or outside or on the circle to do so recall that,
- if
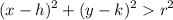 then the given point lies outside the circle
then the given point lies outside the circle - if
 then the given point lies inside the circle
then the given point lies inside the circle - if
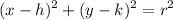 then the given point lies on the circle
then the given point lies on the circle
step-1: define h,k and r
the equation of circle given by
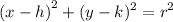
therefore from the question we obtain:
step-2: verify
In this case we can consider the second formula
the given points (-4,2) means that x is -4 and y is 2 and we have already figured out h,k and r² therefore just substitute the value of x,y,h,k and r² to the second formula

simplify parentheses:
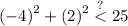
simplify square:
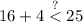
simplify addition:
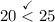
hence,
the point (-4, 2) lies inside the circle