Given equation of the Circle is ,
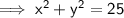
And we need to tell that whether the point (-4,2) lies inside or outside the circle. On converting the equation into Standard form and determinimg the centre of the circle as ,

Here we can say that ,
• Radius = 5 units
• Centre = (0,0)
Finding distance between the two points :-
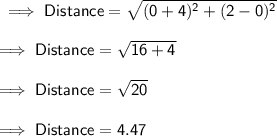
Here we can see that the distance of point from centre is less than the radius.
Hence the point lies within the circle .