Answer:
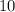 .
.
Explanation:
See below for a proof of why all but the first digit of this
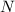 must be "
must be "
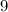 ".
".
Taking that lemma as a fact, assume that there are
 digits in
digits in
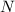 after the first digit,
after the first digit,
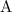 :
:
 , where
, where
 is a positive integer.
is a positive integer.
Sum of these digits:
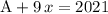 .
.
Since
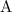 is a digit, it must be an integer between
is a digit, it must be an integer between
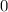 and
and
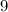 . The only possible value that would ensure
. The only possible value that would ensure
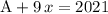 is
is
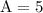 and
and
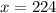 .
.
Therefore:
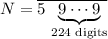 .
.
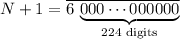 .
.
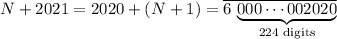 .
.
Hence, the sum of the digits of
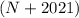 would be
would be
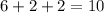 .
.
Lemma: all digits of this
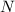 other than the first digit must be "
other than the first digit must be "
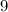 ".
".
Proof:
The question assumes that
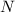 is the smallest positive integer whose sum of digits is
is the smallest positive integer whose sum of digits is
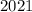 . Assume by contradiction that the claim is not true, such that at least one of the non-leading digits of
. Assume by contradiction that the claim is not true, such that at least one of the non-leading digits of
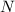 is not "
is not "
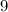 ".
".
For example:
 , where
, where
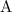 ,
,
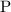 ,
,
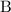 , and
, and
 are digits. (It is easy to show that
are digits. (It is easy to show that
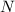 contains at least
contains at least
 digits.) Assume that
digits.) Assume that
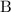 is one of the non-leading non-"
is one of the non-leading non-"
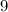 " digits.
" digits.
Either of the following must be true:
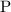 , the digit in front of
, the digit in front of
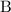 is a "
is a "
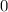 ", or
", or
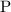 , the digit in front of
, the digit in front of
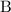 is not a "
is not a "
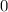 ".
".
If
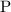 , the digit in front of
, the digit in front of
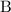 , is a "
, is a "
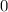 ", then let
", then let
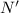 be
be
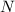 with that "
with that "
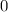 " digit deleted:
" digit deleted:
 .
.
The digits of
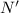 would still add up to
would still add up to
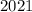 :
:
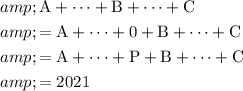 .
.
However, with one fewer digit,
 . This observation would contradict the assumption that
. This observation would contradict the assumption that
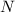 is the smallest positive integer whose digits add up to
is the smallest positive integer whose digits add up to
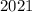 .
.
On the other hand, if
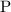 , the digit in front of
, the digit in front of
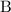 , is not "
, is not "
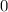 ", then
", then
 would still be a digit.
would still be a digit.
Since
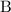 is not the digit
is not the digit
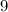 ,
,
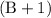 would also be a digit.
would also be a digit.
let
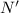 be
be
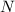 with digit
with digit
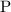 replaced with
replaced with
 , and
, and
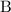 replaced with
replaced with
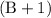 :
:
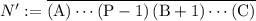 .
.
The digits of
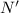 would still add up to
would still add up to
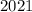 :
:
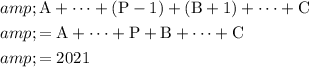 .
.
However, with a smaller digit in place of
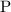 ,
,
 . This observation would also contradict the assumption that
. This observation would also contradict the assumption that
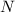 is the smallest positive integer whose digits add up to
is the smallest positive integer whose digits add up to
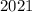 .
.
Either way, there would be a contradiction. Hence, the claim is verified: all digits of this
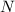 other than the first digit must be "
other than the first digit must be "
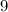 ".
".
Therefore,
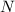 would be in the form:
would be in the form:
 , where
, where
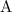 , the leading digit, could also be
, the leading digit, could also be
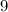 .
.